DeepCrossing

# DeepCrossing

# 1. 动机

这个模型就是一个真正的把深度学习架构应用于推荐系统中的模型了， 2016年由微软提出，完整的解决了特征工程、稀疏向量稠密化，多层神经网络进行优化目标拟合等一系列深度学习再推荐系统的应用问题。这个模型涉及到的技术比较基础，在传统神经网络的基础上加入了embedding，残差连接等思想，且结构比较简单，对初学者复现和学习都比较友好。

DeepCrossing模型应用场景是微软搜索引擎Bing中的搜索广告推荐，用户在输入搜索词之后，搜索引擎除了返回相关结果，还返回与搜索词相关的广告，Deep Crossing的优化目标就是预测对于某一广告，用户是否会点击，依然是点击率预测的一个问题。

这种场景下，我们的输入一般会有类别型特征，比如广告id，和数值型特征，比如广告预算，两种情况。对于类别型特征，我们需要进行one-hot编码处理，而数值型特征一般需要进行归一化处理，这样算是把数据进行了一个简单清洗。 DeepCrossing模型就是利用这些特征向量进行CRT预估，那么它的结构长啥样, 又是怎么做CTR预估的呢？这又是DeepCrossing的核心内容。

# 2. 模型结构及原理

为了完成端到端的训练， DeepCrossing模型要在内部网络结构中解决如下问题：

离散类特征编码后过于稀疏，不利于直接输入神经网络训练，需要解决稀疏特征向量稠密化的问题
如何解决特征自动交叉组合的问题
如何在输出层中达成问题设定的优化目标

DeepCrossing分别设置了不同神经网络层解决上述问题。模型结构如下

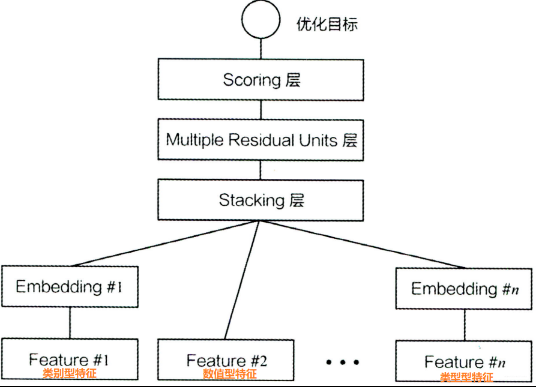
下面分别介绍一下各层的作用：

# 2.1 Embedding Layer

将稀疏的类别型特征转成稠密的Embedding向量，Embedding的维度会远小于原始的稀疏特征向量。 Embedding是NLP里面常用的一种技术，这里的Feature #1表示的类别特征(one-hot编码后的稀疏特征向量）， Feature #2是数值型特征，不用embedding，直接到了Stacking Layer。关于Embedding Layer的实现，往往一个全连接层即可，Tensorflow中有实现好的层可以直接用。和NLP里面的embedding技术异曲同工，比如Word2Vec，语言模型等。

# 2.2 Stacking Layer

这个层是把不同的Embedding特征和数值型特征拼接在一起，形成新的包含全部特征的特征向量，该层通常也称为连接层, 具体的实现如下，先将所有的数值特征拼接起来，然后将所有的Embedding拼接起来，最后将数值特征和Embedding特征拼接起来作为DNN的输入，这里TF是通过Concatnate层进行拼接。

#将所有的dense特征拼接到一起
dense_dnn_list = list(dense_input_dict.values())
dense_dnn_inputs = Concatenate(axis=1)(dense_dnn_list) # B x n (n表示数值特征的数量)

# 因为需要将其与dense特征拼接到一起所以需要Flatten，不进行Flatten的Embedding层输出的维度为：Bx1xdim
sparse_dnn_list = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=True) 

sparse_dnn_inputs = Concatenate(axis=1)(sparse_dnn_list) # B x m*dim (n表示类别特征的数量，dim表示embedding的维度)

# 将dense特征和Sparse特征拼接到一起
dnn_inputs = Concatenate(axis=1)([dense_dnn_inputs, sparse_dnn_inputs]) # B x (n + m*dim)

1
2
3
4
5
6
7
8
9
10
11

# 2.3 Multiple Residual Units Layer

该层的主要结构是MLP，但DeepCrossing采用了残差网络进行的连接。通过多层残差网络对特征向量各个维度充分的交叉组合，使得模型能够抓取更多的非线性特征和组合特征信息，增加模型的表达能力。残差网络结构如下图所示：

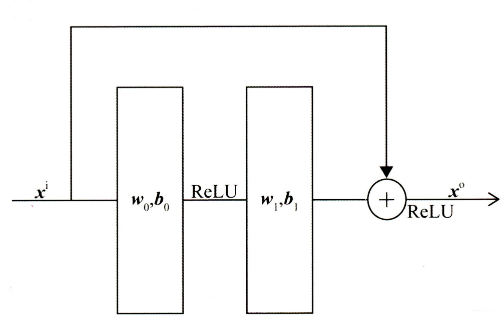
Deep Crossing模型使用稍微修改过的残差单元，它不使用卷积内核，改为了两层神经网络。我们可以看到，残差单元是通过两层ReLU变换再将原输入特征相加回来实现的。具体代码实现如下：

# DNN残差块的定义
class ResidualBlock(Layer):
    def __init__(self, units): # units表示的是DNN隐藏层神经元数量
        super(ResidualBlock, self).__init__()
        self.units = units

    def build(self, input_shape):
        out_dim = input_shape[-1]
        self.dnn1 = Dense(self.units, activation='relu')
        self.dnn2 = Dense(out_dim, activation='relu') # 保证输入的维度和输出的维度一致才能进行残差连接
    def call(self, inputs):
        x = inputs
        x = self.dnn1(x)
        x = self.dnn2(x)
        x = Activation('relu')(x + inputs) # 残差操作
        return x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 2.4 Scoring Layer

这个作为输出层，为了拟合优化目标存在。对于CTR预估二分类问题， Scoring往往采用逻辑回归，模型通过叠加多个残差块加深网络的深度，最后将结果转换成一个概率值输出。

# block_nums表示DNN残差块的数量
def get_dnn_logits(dnn_inputs, block_nums=3):
    dnn_out = dnn_inputs
    for i in range(block_nums):
        dnn_out = ResidualBlock(64)(dnn_out)
    
    # 将dnn的输出转化成logits
    dnn_logits = Dense(1, activation='sigmoid')(dnn_out)

    return dnn_logits

1
2
3
4
5
6
7
8
9
10

# 3. 总结

这就是DeepCrossing的结构了，比较清晰和简单，没有引入特殊的模型结构，只是常规的Embedding+多层神经网络。但这个网络模型的出现，有革命意义。DeepCrossing模型中没有任何人工特征工程的参与，只需要简单的特征处理，原始特征经Embedding Layer输入神经网络层，自主交叉和学习。相比于FM，FFM只具备二阶特征交叉能力的模型，DeepCrossing可以通过调整神经网络的深度进行特征之间的“深度交叉”，这也是Deep Crossing名称的由来。

如果是用于点击率预估模型的损失函数就是对数损失函数：

$$ logloss=-\frac 1N\sum_1^N(y_ilog(p_i)+(1-y_i)log(1-p_i) $$ 其中$$y_i$$表示真实的标签（点击或未点击），$$p_i$$表示Scoring Layer输出的结果。但是在实际应用中，根据不同的需求可以灵活替换为其他目标函数。

# 4. 代码实现

从模型的代码结构上来看，DeepCrossing的模型输入主要由数值特征和类别特征组成，并将经过Embedding之后的类别特征及类别特征拼接在一起，详细的拼接代码如Staking Layer所示，下面是构建模型的核心代码，详细代码参考github。

def DeepCrossing(dnn_feature_columns):
    # 构建输入层，即所有特征对应的Input()层，这里使用字典的形式返回，方便后续构建模型
    dense_input_dict, sparse_input_dict = build_input_layers(dnn_feature_columns)

    # 构建模型的输入层，模型的输入层不能是字典的形式，应该将字典的形式转换成列表的形式
    # 注意：这里实际的输入与Input()层的对应，是通过模型输入时候的字典数据的key与对应name的Input层
    input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
    
    # 构建维度为k的embedding层，这里使用字典的形式返回，方便后面搭建模型
    embedding_layer_dict = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)

    #将所有的dense特征拼接到一起
    dense_dnn_list = list(dense_input_dict.values())
    dense_dnn_inputs = Concatenate(axis=1)(dense_dnn_list) # B x n (n表示数值特征的数量)

    # 因为需要将其与dense特征拼接到一起所以需要Flatten，不进行Flatten的Embedding层输出的维度为：Bx1xdim
    sparse_dnn_list = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=True) 

    sparse_dnn_inputs = Concatenate(axis=1)(sparse_dnn_list) # B x m*dim (n表示类别特征的数量，dim表示embedding的维度)

    # 将dense特征和Sparse特征拼接到一起
    dnn_inputs = Concatenate(axis=1)([dense_dnn_inputs, sparse_dnn_inputs]) # B x (n + m*dim)

    # 输入到dnn中，需要提前定义需要几个残差块
    output_layer = get_dnn_logits(dnn_inputs, block_nums=3)

    model = Model(input_layers, output_layer)
    return model

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

为了方便大家的阅读，我们这里还给大家画了一个整体的模型架构图，帮助大家更好的了解每一块以及前向传播。（画的图不是很规范，先将就看一下，后面我们会统一在优化一下这个手工图）。

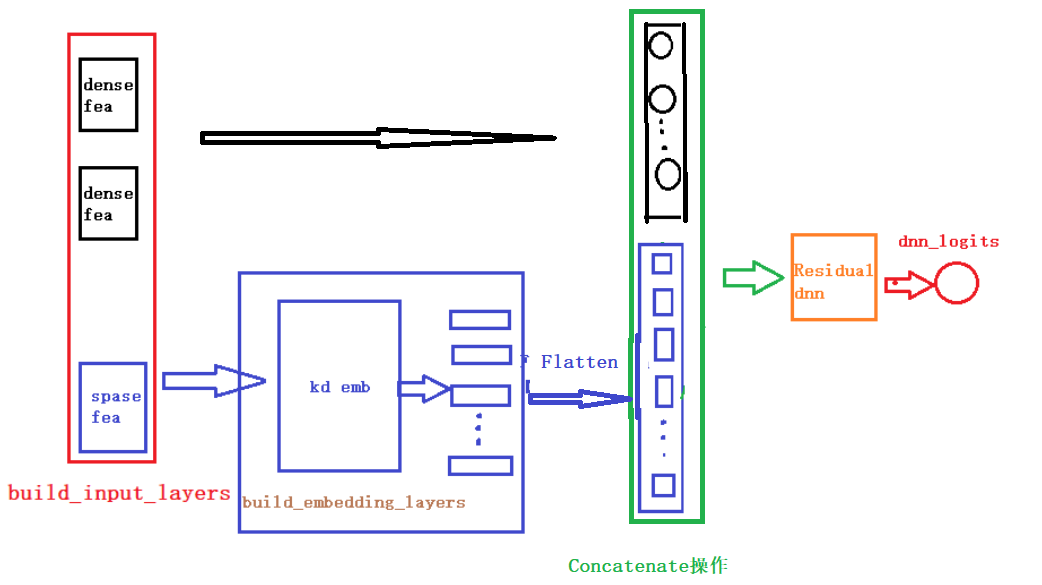
下面是一个通过keras画的模型结构图，为了更好的显示，数值特征和类别特征都只是选择了一小部分，画图的代码也在github中。

DeepCrossing

# 5. 参考资料

编辑

上次更新: 2022/01/04, 02:41:54

← NeuralCF PNN→