1. 简介

逻辑回归作为机器学习领域最基础且常用的模型，掌握逻辑回归的原理推导以及扩展应用是很必要的。从名字上来听，逻辑回归似乎是处理"回归问题"，实际上逻辑回归处理的是分类问题，即 LR 分类器（Logistic Regression Classifier），其数学模型是一个 sigmoid 函数，因图像像 S，又经常称之为 S 形曲线。

sigmoid函数公式： $$ f(x)=\frac{1}{1+e^{-x}} $$ sigmoid函数图像：

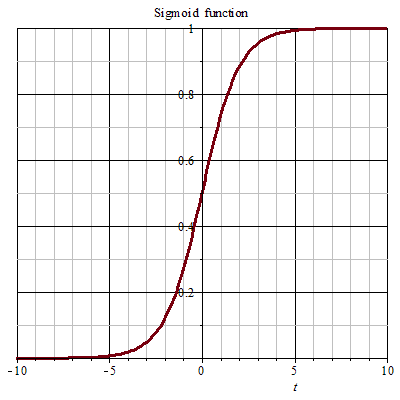
由于 sigmoid 函数的定义域是 $(-∞，+∞)$，而值域为 $(0, 1)$。Logistic 回归通过 sigmoid 联结函数可以将变量映射到 $ (0, 1) $ 之间，这也是为什么最基本的 LR 分类器适合于对二分类（类 0，类 1）目标进行分类。

2. 二项逻辑回归模型

2.1 模型定义

逻辑回归模型在用作二分类时，模型的表达式如下： $$ p_i(y_i=1 \mid x_i) = \frac{1}{1+e^{-w x_i}} \ \ p_i(y_i=0 \mid x_i) = \frac{e^{-w x_i}}{1+e^{-w x_i}} $$ 其中，随机变量$x_i \in \mathbb{R}^{n}$为实数，随机变量$y_i$的取值为${0, 1}$，参数$w\in \mathbb{R}^{n}$。$wx_i$表示变量$x_i$与参数$w$之间的内积。

由逻辑回归模型的表达式可知，其输出值的范围为$(0,1)$。这里以$p_i(y_i=1 \mid x_i)$举例：

• 由于内积$-wx_i$的取值范围为$(-∞，+∞)$，可知分母项$1+e^{wx_i}$取值范围是$(1, +∞)$；
• 最后可得，分母项的倒数范围就是$(0,1)$；

2.2 几率

最开始我们提到，逻辑回归和线性回归最本质的区别就是它们分别是分类和回归模型，这是属于两个不同的任务。那么为什么逻辑回归会包含“回归”两个字呢？回答这个问题前，先来弄明白几率的概念。

几率就是事件发生的概率和事件不发生的比值： $$ \eta_{i}=\frac{p_{i}}{1-p_{i}} $$ 现在，我们通过线性模型来拟合几率$\eta_{i}$的对数，有： $$ wx_i=\log(\frac{p_{i}}{1-p_{i}}) $$ 将等式两边化为以e为底的指数函数，有： $$ e^{wx_i} =\frac{p_{i}}{1-p_{i}} \ \Downarrow \ p_i = \frac{1}{1+e^{-w x_i}} $$ 可以看到，逻辑回归本质上就是关于事件几率的线性回归。当然，逻辑回归和线性回归存在本质上的不同，其次在损失函数上，线性回归中的损失函数是均方误差，而 Logistic 回归的损失函数是负对数似然（Negative Log-Likelihood）。

二者的共同之处在于，他们的损失函数都是通过最大似然估计推导而来，其次在求解参数的过程中都可以使用梯度下降法，可参考资料[2]。

2.3 模型假设

逻辑回归模型的基本假设是$y_i$服从伯努利分布，也称为两点分布或者$0-1$分布。即： $$ \begin{array}{c}

p_i(y_i=1 \mid x_i ; w)=p_i \ \ p_i(y_i=0 \mid x_i ; w)=1-p_i

\end{array} $$ 将公式写在一起有： $$ p_i(y_i \mid x_i ; w)=p_i^{y_i}\left(1-p_i\right)^{1-y_i} $$

2.4 模型参数估计

我们可以通过使用最大似然估计法来估计二项逻辑回归模型的参数，设似然函数为： $$ \prod_{i=1}^{n}p_{i}^{y_{i}}·\left(1-p_{i}\right)^{1-y_{i}} $$ 对似然函数取对数后加负号有： $$ L(w)=-\sum_{i=1}^{n}\left(y_{i} \log \left(p_{i}\right)+\left(1-y_{i}\right) \log \left(1-p_{i}\right)\right) $$ 我们可以通过最大化似然函数来对参数进行估计，在这里等价于最小化负对数似然函数 $L(w)$，同样可以得到 $w$ 的估计值。

下面关于 $L(w)$ 对 $w$ 求导，具体步骤如下：

1. 对于任意样本$x_i$，有：

$$ \begin{aligned} l &=-y_{i} \log \left(p_{i}\right)-\left(1-y_{i}\right) \log \left(1-p_{i}\right) \ \ &=-y_{i} \log \left(p_{i}\right)-\log \left(1-p_{i}\right)+y_{i} \log \left(1-p_{i}\right) \ \ &=-y_{i}\left(\log \left(\frac{p_{i}}{1-p_{i}}\right)\right)-\log \left(1-p_{i}\right) \end{aligned} $$ 2. 由于几率 $\eta_{i}=\frac{p_{i}}{1-p_{i}}$，可得 ${p_i}=\frac{\eta_{i}}{1+\eta_{i}}$，代入：

$$ \begin{aligned} l &=-y_{i} \log \left(\eta_{i}\right)-\log \left(1-\frac{\eta_{i}}{1+\eta_{i}}\right) \ \ &=-y_{i} \log \left(\eta_{i}\right)+\log \left({1+\eta_{i}}\right) \ \ &=-y_{i} \log \left(\eta_{i}\right)+\log \left(1+e^{\log \left(\eta_{i}\right)}\right) \end{aligned} $$ 3. 对几率的对数 $\log(\eta_{i})$ 求导：

$$ \frac{d l}{d \log \left(\eta_{i}\right)}=-y_{i}+\frac{e^{\log \left(\eta_{i}\right)}}{1+e^{\log \left(\eta_{i}\right)}}=-y_{i}+p_{i} $$

​ 前面我们提到过，逻辑回归相当于事件的对数几率拟合线性回归，即：$\log \left(\eta_{i}\right)=\log \frac{p_{i}}{1-p_{i}}=wx_i$，代入有： $$ \frac{d l}{d \log \left(\eta_{i}\right)} =\frac{d l}{d (wx_i)}==-y_{i}+p_{i} \ \Downarrow \ \frac{d l}{dw}=(-y_{i}+p_{i})x_i $$ 4. 由于我们的目标是最小化负对数似然函数，所以采梯度下降方向：

$$ w \leftarrow w-\frac{\gamma}{n} \sum_{i=1}^{n}\left(-y_{i}+p_{i}\right) x_{i} \ 其中，\gamma为学习率 $$

3. 从广义线性模型推导逻辑回归

无论是线性回归还是逻辑回归，它们都是广义线性模型（Generalize Linear Model, GLM）的一种特殊形式。本小节将从广义线性模型的角度来对逻辑回归模型进行推导。

先给出本小节的参考链接，如有说的不对的地方，欢迎批评指正。

指数分布：

指数族分布：https://blog.csdn.net/qq_27388259/article/details/113011862

统一分布：指数模型家族：https://zhuanlan.zhihu.com/p/148776108

指数族分布|机器学习推导系列（九）：https://zhuanlan.zhihu.com/p/315688850

广义线性模型：

从「一」到「无穷大」：广义线性模型 (GLM)：https://zhuanlan.zhihu.com/p/149691129

广义线性模型（Generalized Linear Model）：https://zhuanlan.zhihu.com/p/22876460

从广义线性模型(GLM)理解逻辑回归：https://fighterhit.github.io/2017/12/24/machine_learning_notes/从广义线性模型理解逻辑回归/ (opens new window)

3.1指数分布族

在介绍广义线性模型之前，需要先来了解指数分布，因为指数分布是后面介绍的广义线性模型的基本假设之一。

指数族分布(exponential family)是指一类分布，包括高斯分布、伯努利分布、二项分布、泊松分布、伽马分布、贝塔分布等。很多数学模型都是建立在某种或某几种分布上的，比如风控金融判断好人坏人的伯努利分布，线性回归模型的高斯分布等。

在指数分布族中，每一类分布都可以使用如下的公式表示： $$ p(y\mid \eta)=h(y) \exp \left(\eta^{T} T(y)-a(\eta)\right) $$ 这里我需要提醒一下数学基础跟我一样不牢固的同学，这里的指数族分布的表达式指的概率分布函数。本人一直将概率密度函数和概率分布函数混淆。这里说明一下它们之间的关系：

• 在连续函数中，概率分布函数$F(x)$与概率密度函数$f(x)$的关系为：$F(x)=\int_{-\infty}^{x} f(x) d x$；
• 概率密度函数还有一个性质：$f(x) \geq 0, \int_{-\infty}^{\infty} f(x) d x=1$；

OK，现在回到前面指数分布的表达式，各参数含义如下：

• $\eta$：自然参数，不同的指数分布参数不同；
• $T(y)$：充分统计量（Sufficient Statistic），一般有 $T(y)=y$ ；
• $a(\eta)$：对数配分函数（Log Partition Function）；
• $h(y)$：$h(y)\geq 0$，一般取值为1；

下面详细解释：

（1）什么是充分统计量？

定义：设 $ x_{1}, x_{2}, \cdots, x_{n}$ 是个总体的样本,总体分布函数为$ F(x ; \theta) $, 统计量 $ \Phi(x)=\Phi\left(x_{1}, x_{2}, \cdots, x_{n}\right)$ 称为 $\theta $ 的充分统计量,如果在给定 $\Phi(x) $ 的取值后, $x_{1}, x_{2}, \cdots, x_{n} $ 的条件分布与$ \theta $ 无关。

比如对于服从高斯分布的样本集，我们无需记录所有样本，只需记录它们的均值和方差即可。

（2）对数配分函数

前面介绍了概率密度函数的一个性质：$f(x) \geq 0, \int_{-\infty}^{\infty} f(x) d x=1$。

若指数分布族没加上归一化因子 $a(\eta)$，则分布函数 $\hat{p}(y\mid \eta)=h(y) \exp \left(\eta^{T} T(y)\right)$ 可能大于1，这是显然的，画出指数函数图像就知道了。原因很简单，就是分布函数对应的密度函数 $\hat{f}( y \mid \theta)$ 在区间的积分大于1了。

对于这种情况，我们希望通过除以一个归一化 $Z$ 来将积分值的区间缩放到 $(0,1)$： $$ \begin{array}{c} \int \frac{1}{Z} \hat{f}(y \mid \eta) \mathrm{d} y =1 \ \Downarrow \ Z=\int \hat{f}(y \mid \eta) \mathrm{d} y \end{array} $$ 在明白这一点后，现在我们对指数分布函数 $p(y\mid \eta)$ 化简： $$ \begin{array}{c} p(y \mid \eta)=h(y) \exp \left(\eta^{T} T(y)-A(\eta)\right) \ \Downarrow

\ p(y \mid \eta)=\frac{1}{\exp (A(\eta))} h(y) \exp \left(\eta^{T} T(y)\right)= \frac{1}{Z} \hat{p}(y \mid \eta) \ \Downarrow

\ A(\eta)=\log Z

\end{array} $$ 归一化因子又称作配分函数，这也是$A(\eta)$叫做对数配分函数的原因。

3.2 广义线性模型假设

上一小节主要介绍了指数分布族，旨在了解指数分布函数的形式以及各参数的意义。

本小节将要介绍的广义线性模型，它的构建基于3个假设：

1. 变量$y$的条件概率服从指数分布族，即 $y \mid x ; \theta \sim \text { ExponentialFamily }(\eta)$；
2. 在给变量 $x$下，广义线性模型的求解目标为 $T(y)|x$；考虑到大多数情况下 $T(y)=y$，所以求解目标为 $h(x)=E(y \mid x)$；
3. 自然参数$\eta$和变量$x$为线性关系：$\eta=\theta^{T}x$，若 $\theta$ 为向量，则$\eta_i=\theta_i^{T}x$；

3.3 广义线性模型推到逻辑回归

前面我们提到过，逻辑回归的基本假设为变量$y$服从伯努利分布，这满足第一个假设： $$ \begin{flalign}

& p(y=1 \mid x ; \theta)=p \ \ & p(y=0 \mid x ; \theta)=1-p

\end{flalign} $$ 合并公式，进一步有： $$ \begin{aligned} p(y \mid x ; \theta) &=p^{y}(1-p)^{1-y} \ \ &=\exp \left(\log p^{y}(1-p)^{1-y}\right) \ \ &=\exp (y \log p+(1-y) \log (1-p)) \ \ &=\exp \left(\log \left(\frac{p}{1-p}\right) y+\log (1-p)\right) \end{aligned} $$ 参照前面的指数分布族函数： $$ p(y\mid \eta)=h(y) \exp \left(\eta^{T} T(y)-a(\eta)\right) $$ 可得： $$ \begin{flalign} &h(y)=1 \ \ &\eta=\log \left(\frac{p}{1-p}\right) \Rightarrow p = \frac{1}{1+e^{-\eta}} \ \ &T(y)=y \ \ &a(\eta)=\log (1-p) \end{flalign} $$

最后，再根据第三个假设 $\eta=\theta^{T}x$ ，代入 $p$ 的表达式有： $$ \begin{array}{c}

p(y=1 \mid x ; \theta) = \frac{1}{1+e^{-\theta^{T}x}} \ \Leftrightarrow \ p(y_i=1 \mid x_i ; \theta) = \frac{1}{1+e^{-\theta^{T}x_i}}

\end{array} $$ 至此，从广义线性模型推到逻辑回归的过程结束。

同样的，还可以从高斯分布的角度来推到出线性回归模型，这里不再推导，详可见参考的前面的博客。

4. 推荐中的逻辑回归

4.1 LR模型

我们在前面介绍了二项逻辑回归模型，当将样本的特征输入到模型后，输出的值范围在$(0,1)$之间。在推荐的点击预测业务中，用户对物品的点击行为只存在两个可能{0: 未点击，1：点击}，实际就是一个二分类的问题。

当我们将与用户、物品以及其它相关的特征信息输入到逻辑回归模型后，得到的输出就可以作为用户对物品的点击概率。在优化模型时，损失函数与前面提到的一样为负对数似然函数，再通过梯度下降法进行参数优化。

下面分析一下逻辑回归模型的优缺点。

• 优点：
  • LR模型形式简单，可解释性好，预测结果是界于 0 和 1 之间的概率，可直接理解为用户的点击概率。
  • 适用于连续性或者离散型数据。
  • 模型简单，易于实现，同时训练的开销小，训练速度快。
• 缺点：
  • 表达能力不强， 无法进行特征交叉， 特征筛选等一系列“高级“操作需要人工进行组合， 可能造成信息的损失。
  • 处理非线性问题能力差。
  • 很难处理数据不平衡问题。

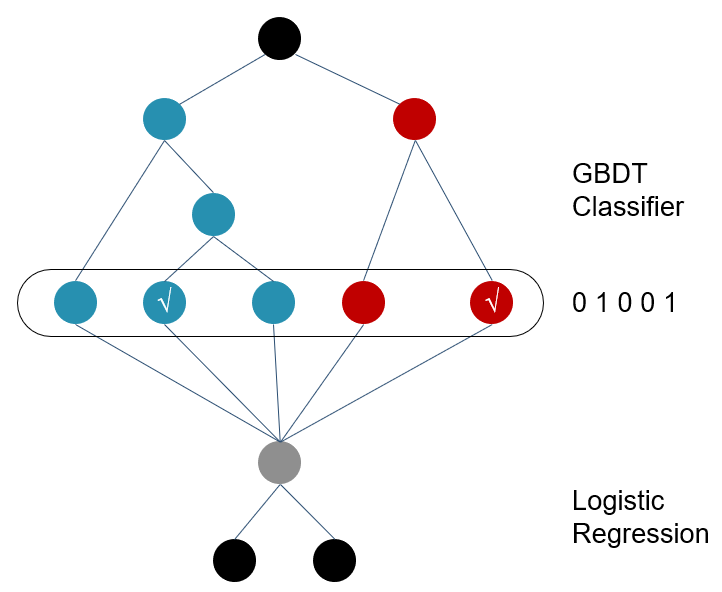
4.2 GBDT+LR

前面我们提到了LR模型的特征表达能力不足，需要通过人工进行特征筛选和特征组合，而这将导致人工的成本过高，同时会造成信息损失。因此，对模型中引入自动特征筛选、组合是有必要的。

由于GBDT的思想使其具有天然优势，可以发现多种有区分性的特征及特征组合。在这种背景下，Faceook于2014年发布了应用于广告推荐的GBDT+LR模型，利用GBDT自动进行特征筛选和组合， 进而生成新的离散特征向量， 再把该特征向量当做LR模型的输入， 来产生最后的预测结果。

关于该模型的详细原理和实现，可以参考资料[4]。

参考资料

[1] 《百面机器学习》，诸葛越著

[2] 最大似然估计：从概率角度理解线性回归的优化目标：https://zhuanlan.zhihu.com/p/143416436

[3] Logistic回归：https://lumingdong.cn/logistic-regression.html

[4] 逻辑回归模型与GBDT+LR：https://zhongqiang.blog.csdn.net/article/details/108349729

[5] 线性回归、logistic回归、广义线性模型: https://blog.csdn.net/sinat_37965706/article/details/69204397