1. 基础数学知识

1.1 凸优化

本小节将简单介绍凸优化问题，如果想进一步了解与凸优化相关的知识，可参考参考链接中斯坦福课程对应的课件。

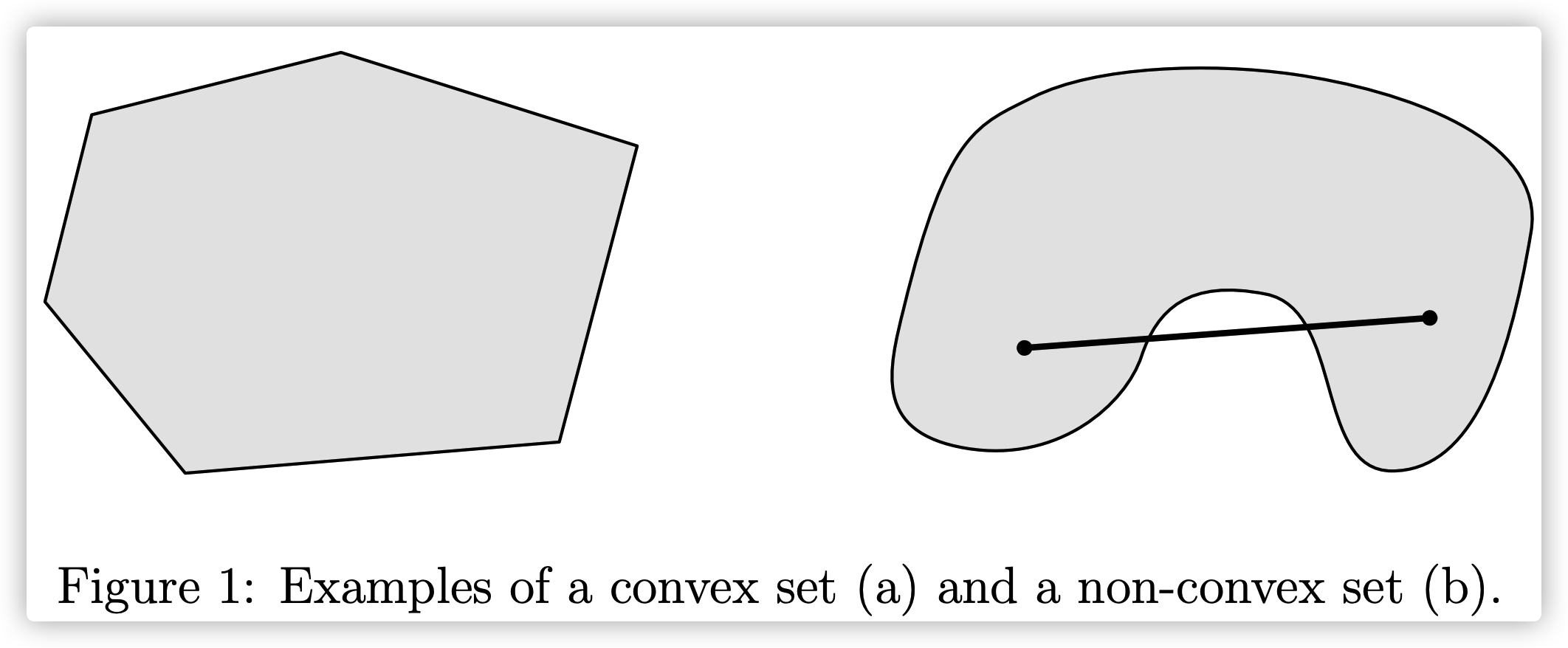
1.1.1 凸集

如果集合 $S$ 为凸集，则对于任意 $x,y \in S$ 以及 $\theta \in \mathbb{R}$，其中 $0 \leq \theta \leq 1$ ，有： $$ \theta x+(1-\theta) y \in S $$

1.1.2 凸函数

函数 $f(\cdot)$ 为凸函数当且仅当对定义域中的任意两点 $x,y$ 和任意实数 $\lambda \in [0,1]$ 有： $$ f(\lambda x+(1-\lambda)y) \le \lambda f(x)+(1-\lambda)f(y) $$ 直观上来看，对于 $z \in (x, y)$，对应的坐标点 $\left (z,f(z)\right)$ 的位置，均处于点 $(x, f(x))$ 和点 $(y,f(y))$ 连接成的线段的下方。

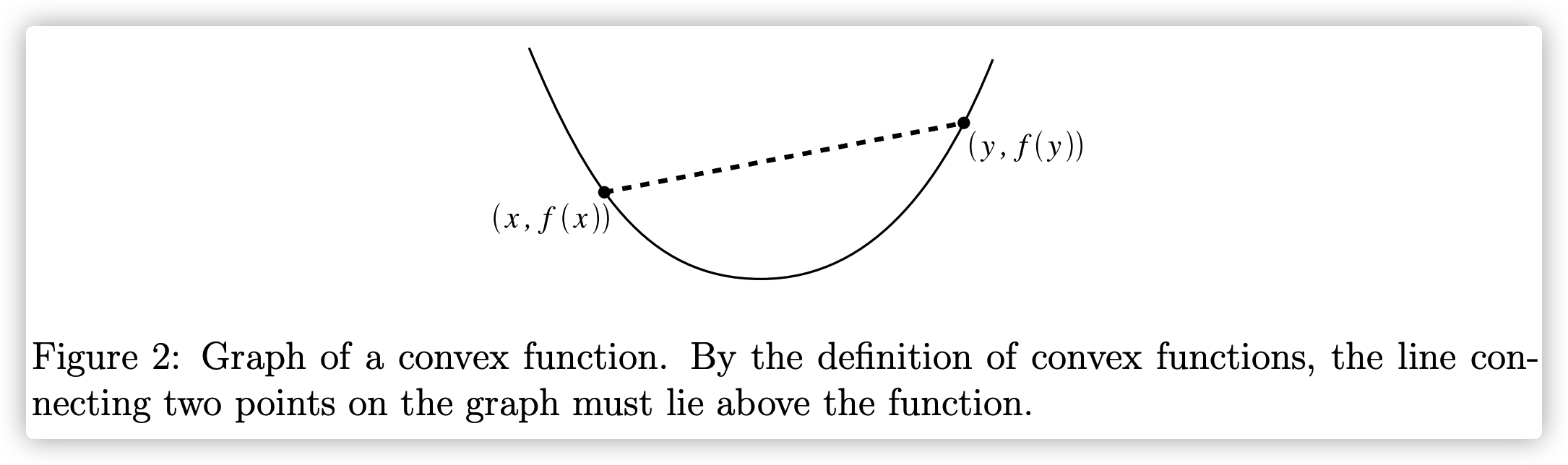
凸函数具有一个重要的性质： 局部极小值点为全局极小值点。

1.1.3 凸函数的判定

我们可以通过一阶条件和二阶条件来判定目标函数是否为凸函数。

一阶条件

设 $f(x)$ 在凸集$S$ 上有一阶连续偏导数，则 $f(x)$ 为 $S$ 上的凸函数的充要条件为：对于任意两个不同的点 $x_1,x_2$ 有： $$ f\left(x_1\right) \geq f\left(x_2\right)+\nabla f\left(x_2\right)^{T}\left(x_2-x_1\right) $$ 二阶条件

设 $f(x)$ 在凸集 $\mathrm{S} $ 上有二阶连续偏导数, 则 $ f(x) $ 为 $ \mathrm{S} $ 上的凸函数的充要条件为: $ f(x) $ 的 $Hessian$ 矩阵 $ \nabla^{2} f(x)$ 在 $S$ 上处处半正定。

假如 $Hessian$ 矩阵 $\nabla^{2} f(x) $ 在 $S$ 上处处正定, 则 $ f(x)$ 严格凸函数, 但是反过来不成立。

其中，$Hessian$ 矩阵和正定矩阵定义如下：

• $Hessian$ 矩阵

$$ \nabla^{2} f(x)=\left(\begin{array}{cccc} \frac{\partial^{2} f(x)}{\partial^{2} x_{1}} & \frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{n}} \ \frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f(x)}{\partial^{2} x_{2}} & \cdots & \frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{n}} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f(x)}{\partial^{2} x_{n}} \end{array}\right) $$

• 正定矩阵

  • 定义：特征值都大于 $0$ 的实对称矩阵；
  • 充分必要条件：所有各阶顺序主子式都大于 $0$ ，即 $\operatorname{det} \boldsymbol{A}_{i}>0 \quad(i=1,2, \cdots, n)$；

• 半正定矩阵

  • 定义：特征值都不小于 $0$ 的实对称矩阵；
  • 充分必要条件：$\operatorname{det} \boldsymbol{A}{i}=0$ 且 $\operatorname{det} \boldsymbol{A}{i}\ge 0 \quad(i=1,2, \cdots, n-1)$；

1.1.4 凸优化问题

对于优化的目标函数为凸函数的问题，我们称为凸优化问题。一些常用的机器学习模型，如逻辑回归、支持向量机、线性回归模型等，对应的优化问题就是凸优化问题。前面我们提到过，对于凸函数它的局部极小值即为全局最小值，所以这类问题一般被认为是比较容易求解的问题。

非凸优化问题包括了主成分分析问题，矩阵分解，深度神经网络等。

1.2. 极值

1.2.1 一元函数

在微积分中，函数$f(x)$在点 $x_0$ 处的导数定义为： $$ f^{\prime}\left(x_{0}\right)=\lim {x \rightarrow x{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} $$ 它在几何上就是指函数 $f(x)$ 在 $x_0$ 上切线方向。一般而言，如果要计算某个函数 $f(x)$ 的最大值或者最小值。通常先计算它的导数 $f'(x)$， 然后求解方程 $f'(x)=0$ 可以得到函数的临界点，进一步判断临界点是否为最大值或者最小值。但是临界点并不一定是全局最大值或者全局最小值，甚至不是局部的最大值或者局部最小值。

例如: 函数 $f(x)=x^{3}$ ，它的导数是 $f^{\prime}(x)=3 x^{2}$ ，因此 $x=0$ 是它的临界点。但 $x=0$ 则不是这个函数的局部最大值或者局部最小值点，因为 $f(x)<0$, $\forall x<0$ 且 $f(x)>0, \forall x>0 $ 。

下面介绍极值点（局部最值）的判断条件：

极值点判定的第一充分条件

• 如果 $x \in\left(x_{0}-\delta, x_{0}\right)$ ，有 $f^{\prime}(x)>0$ ; 而 $x \in\left(x_{0}, x_{0}+\delta\right) $，有 $f^{\prime}(x)<0$ , 则 $f(x)$ 在 处取得极大值；
• 如果 $x \in\left(x_{0}-\delta, x_{0}\right)$ ，有 $f^{\prime}(x)<0$ ; 而 $x \in\left(x_{0}, x_{0}+\delta\right) $，有 $f^{\prime}(x)>0$ , 则 $f(x)$ 在 处取得极小值；
• 如果当 $x \in\left(x_{0}-\delta, x_{0}\right) $ 及 $ x \in\left(x_{0}, x_{0}+\delta\right) $ 时, $f^{\prime}(x) $ 符号相同, 则 $ f(x)$ 在 $ x_{0}$ 处无极值；

极值点判定的第二充分条件

从 $Taylor$ 级数的角度来看，$f(x)$ 在 $x_0$ 附件的 $Taylor$ 级数为： $$ f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2}\left(x-x_{0}\right)^{2}+O\left(\left|x-x_{0}\right|^{3}\right) $$ 若 $f(x)$ 在 $ x_{0}$ 处具有二阶导数, 且 $f^{\prime}\left(x_{0}\right)=0, f^{\prime \prime}\left(x_{0}\right) \neq 0 $，有：

• 当 $f^{\prime \prime}\left(x_{0}\right)<0$ 时, 函数 $f(x)$ 在 $ x_{0} $ 处取得极大值;
• 当 $f^{\prime \prime}\left(x_{0}\right)>0$ 时, 函数 $f(x) $ 在 $x_{0}$ 处取得极小值;

1.2.2 多元函数

对于多元函数 $f(\mathbf{x})=f(x_1, ..., x_n)$ ，它的梯度可以定义为： $$ \nabla f(\mathbf{x})=\left(\frac{\partial f}{\partial x_{1}}(\mathbf{x}), \cdots, \frac{\partial f}{\partial x_{n}}(\mathbf{x})\right) $$ 多元函数 $f(\mathbf{x})$ 在点 $\mathbf{x_0}$ 处的 $Taylor$ 级数为： $$ f(\mathbf{x})=f\left(\mathbf{x}{0}\right)+\nabla f\left(\mathbf{x}{0}\right)\left(\mathbf{x}-\mathbf{x}{0}\right)+\frac{1}{2}\left(\mathbf{x}-\mathbf{x}{0}\right)^{T} \mathbf{H}\left(\mathbf{x}-\mathbf{x}{0}\right)+O\left(\left|\mathbf{x}-\mathbf{x}{0}\right|^{3}\right) $$ 其中，$\mathbf{H}$ 表示 $Hessian$ 矩阵。

判定条件为：

• 如果 $x_0$ 是临界点，并且 $Hessian$ 矩阵为正定矩阵时， $f(\mathbf{x})$ 在 $\mathbf{x_0}$ 处达到局部极小值。
• 如果 $x_0$ 是临界点，并且 $Hessian$ 矩阵为负定矩阵时， $f(\mathbf{x})$ 在 $\mathbf{x_0}$ 处达到局部极大值。
• 如果 $x_0$ 是临界点，但是 $Hessian$ 矩阵为不定矩阵时， $f(\mathbf{x})$ 在 $\mathbf{x_0}$ 处不取极值。

负定矩阵：

• 定义：特征值都小于 $0$ 的实对称矩阵；

• 充分必要条件： $$ \operatorname{det} \boldsymbol{A}_{i}\left{\begin{array}{l} <0(i \text { 为奇数 }) \

  0(i \text { 为偶数 }) \end{array}(i=1,2, \cdots, n)\right. $$

相关证明可以文末的引用资料。

2. 损失函数

在监督学习中，损失函数来画了模型和训练样本的匹配程度。例如，对于训练样本 $(x_i, y_i)$，其中 $x_i\in X$ 表示第 $i$ 个样本的特征，$y_i \in Y$ 表示该样本点的标签。参数为为$\theta$的模型可以表示为函数 $f(\cdot,\theta):X \to Y$ ，模型关于第 $i$ 个样本点的输出为 $f(x_i, \theta)$。

为了刻画模型输出和样本标签之间的匹配程度，定义损失函数 $L(\cdot,\cdot):Y \times Y \to \mathbb{R}_{\Bbb\ge 0}$ ，$L(f(x_i,\theta),y_i)$ 越小，表明模型在该样本点匹配的程度越好。

在机器学习中，优化问题的损失函数可以表示为： $$ L(\theta) = \mathbb{E}{(x,y)\sim P{data}}L(f(x, \theta),y) $$ 其中，$x$ 表示模型输入数据，$y$ 表示模型期望的输出，$f(x,\theta)$ 表示模型的实际输出。

我们希望通过不断优化参数 $\theta$，来最小化损失函数 $L(\theta)$ 的值，这就是优化问题的求解。 $$ \theta^*=\rm{arg}\ minL(\theta) $$

3. 常见优化算法

从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。那么，如果想计算一个函数的最小值，就可以使用梯度下降法的思想来做。

假设求解目标函数为 $L(\theta)=L(\theta_1, ..., \theta_n)$ 的最小值，可以从一个初始点 $\theta^{0}=(\theta_1^{(0)},...,\theta_n^{(0)})$，基于学习率 $\eta>0 $ 构建迭代过程： $$ \begin{array}{l} \theta_{1}^{(i+1)}=\theta_{1}^{(i)}-\eta \cdot \frac{\partial L}{\partial \theta_{1}}\left(\theta^{(i)}\right) \ \cdots \ \theta_{n}^{(i+1)}=\theta_{n}^{(i)}-\eta \cdot \frac{\partial L}{\partial \theta_{n}}\left(\theta^{(i)}\right) \end{array} $$ 一旦达到收敛条件的话，迭代就结束。从梯度下降法的迭代公式来看，下一个点的选择与当前点的位置和它的梯度相关。

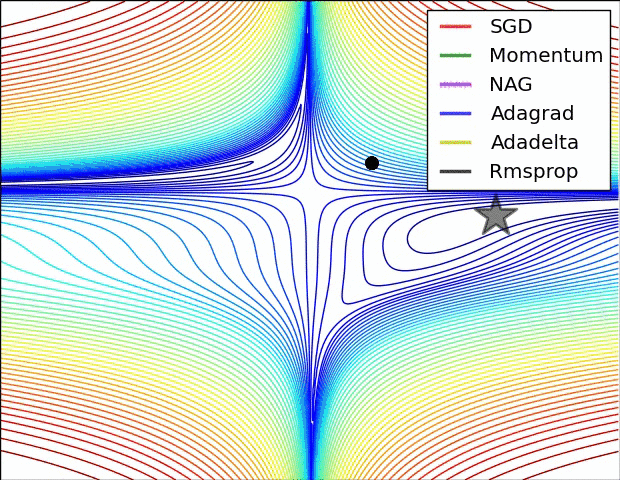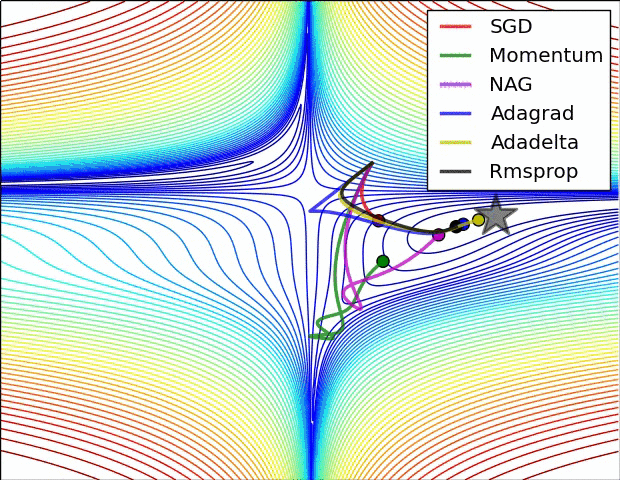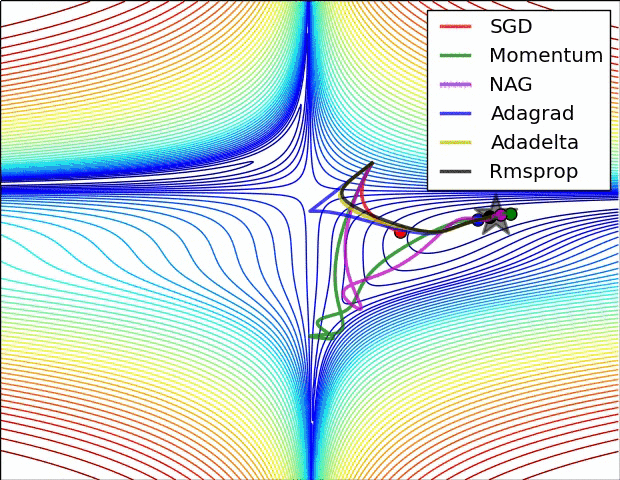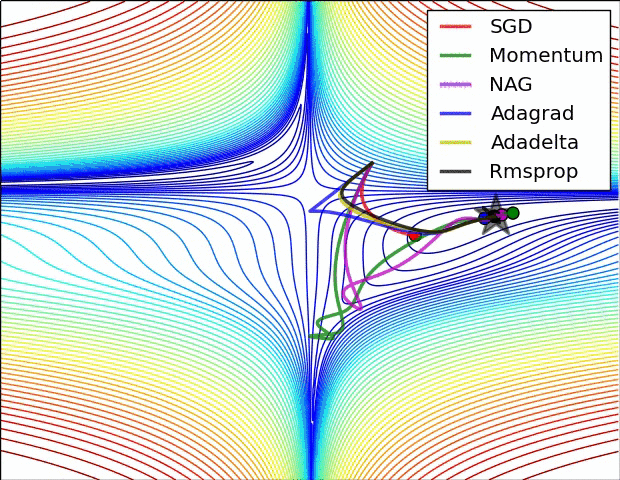
不同的优化算法，由于优化目标函数时有着不同的出发点，所以函数在寻找局部极小值点的时对应的轨迹也有所不同。

3.1 BGD

经典的梯度下降法是采用训练集数据的平均损失来近似目标函数，这种方法被称为批量梯度下降法（Batch Gradient Descent，BGD）。损失函数及梯度的计算公式如下： $$ L(\theta) = \frac{1}{N} \sum_{i=1}^{N} L(f(x, \theta),y) \ \nabla L(\theta) = \frac{1}{N} \sum_{i=1}^{N}\nabla L(f(x, \theta),y) $$ 模型参数的更新公式为： $$ \theta = \theta- \alpha\nabla L(\theta) $$ 其中，$\alpha$ 为学习率。可以看出，为了获得准确的梯度，批量梯度下降法每一步都将整个数据集载入进行计算，时间花费和内存开销都非常大，无法应用于大数据集和大规模场景。

3.2 SGD

SGD的英文全称是 Stochastic Gradient Descent，中文名为随机梯度下降法。随机梯度下降法是使用单个训练数据来近似平均损失： $$ L(\theta;x_i,y_i) = L(f(x_i, \theta),y_i) \ \ \nabla L(\theta) = \nabla L(f(x_i, \theta),y_i) $$ 随机梯度下降法放弃了对梯度准确性的追求，每步仅随机采样一个样本来估计梯度，优点是计算速度快，内存开销小。但是由于每一步接收的信息量有限，随机梯度下降法对梯度的估计常常出现偏差，造成目标函数的收敛不稳定，伴有剧烈波动，甚至出现不收敛的情况。

对于随机梯度下降法而言， 除了存在会陷入局部最优解的困境，更害怕的是遇到山谷和鞍点两种地形。

• 山谷顾名思义就是一条狭长的山间小道，左右为峭壁。在山谷中，准确的梯度方向是沿山道向下，但是粗略的梯度估计会使得它在两山壁之间来回反弹震荡，造成收敛不稳定和收敛速度慢。
• 鞍点就是形状似马鞍，一个方向上两头翘，另一个方向两头垂，中间是一片平原。在鞍点处，随机梯度下降法会陷入平原，但是距离最低点还有很远。在梯度接近为 $0$ 处，随机梯度下降法无法察觉出梯度的变化，结果就会陷入停滞状态。

3.3 MBGD

MBGD的全称是 Mini-Batch Gradient Descent，中文名为小批量梯度下降法。它是是一种介于BGD和SGD之间的优化算法。前面介绍的BGD和SGD算法，各自存在不同的优缺点，BGD梯度估计更准确但时间开销更大，SGD计算开销小却存在不稳定的缺点。

为了缓解二者各存在的问题，小批量梯度下降法每次在更新梯度的时候，只需要同时处理 $n(n<<N)$ 个训练数据，目标函数及梯度计算公式下： $$ L(\theta) = \frac{1}{n} \sum_{i=1}^{n} L(f(x_i, \theta),y_i) \ \nabla L(\theta) = \frac{1}{n} \sum_{i=1}^{n}\nabla L(f(x_i, \theta),y_i) $$

这里存在两个问题：

• 如何选取参数 $n$？在不同的场景中，最优参数 $n$ 会不一样，需要通过调参来设定，一般都会取 $2$ 的幂次方，因为这可以充分利用矩阵的运算操作。

• 如何挑取 $n$ 个数据?为了避免数据特定顺序的影响，一般先要将数据进行随机排序，然后迭代时在按顺序挑选 $n$ 个数据。

3.4 Momentum

前面提到SGD算法存在山谷震荡和鞍点停滞的问题，在解决这两个问题之前。先做一个思维实验。我们分别想象一个纸团和铁球从山顶往下滚。

• 假如遇到的是山谷地形。纸团由于质量小，在山谷中滚动过程中极易受到山壁弹力的影响，从而来回震荡，这有点类似于随机梯度下降法在梯度更新时的不稳定。而铁球由于自身质量大，在下降过程中受到山壁弹力的干扰小，从而平稳地滚到山底。
• 假如遇到的是鞍点地形。纸团在进入平原时，由于质量小导致惯性也较小，容易停滞不前。而铁球由于自身惯性较大，在来到鞍点中心时，也有一定机会冲出去平坦的陷阱。

从上述情况综合看来，铁球由于自身质量较大，在下降过程中即便有受到其它方向的力，但是惯性却使得它的运动轨迹不易出现山谷震荡和鞍点停滞的情况。由此，我们引入动量法（Momentum），目的在于保留前面提到的惯性：

$$ \begin{array}{c} v_t = \alpha v_{t-1} + \eta \frac{\partial L}{\partial \theta} \ \ \theta_{t+1} = \theta_{t} - v_t \end{array} $$

参数的更新方向由两部分组成：

• 参数$\alpha$乘以一时刻前进信息 $v_{t-1}$。参数 $\alpha$ 作用类似于阻力，通过它可以控制保留多少前一时刻的梯度信息。
• 学习率$\eta$乘以损失函数当前梯度。

可以看出，梯度更新方向 $v_t$ 同时依赖于 $v_{t-1} 和 $$\frac{\partial L}{\partial \theta}$，增加了上一次前进信息的利用。这根我们在物理中计算当前速度时一个道理，同时考虑前一时刻的速度和当前加速度。

回到前面介绍的铁球实验。沿着山谷向下的铁球，会同时受到沿坡道向下的力和左右山谷碰撞的力。由于向下的力稳定不变，产生的动量不断累加，左右的弹力来回摇摆，动量在累积后相互抵消，从而减弱了铁球来回的震荡。

这里的动量法由于引入了惯性，所以它的参数轨迹类似铁球下山的轨迹。而随机梯度下降法则与纸团下山的轨迹类似，震荡不稳定。因此，相比较于随机梯度下降法，动量法收敛速度更快，收敛曲线也更稳定。

​

3.5 AdaGrad

当我们在对模型进行参数优化时，学习率的设定也是很重要的。如果学习率过小，训练时会耗费大量时间，过大会导致训练无法收敛。为了加快收敛速度，同时又提高求解精度，通常会采用衰减学习率的方案：一开始算法采用较大的学习率，在误差曲线平缓以后，减小学习率做出更精细的调整。

随机梯度下降法对环境的感知是指在参数空间中，根据不同参数的经验性判断，自适应地确定参数的学习率，不同参数的在更新时更新的步长不一样。例如，在推荐系统中，如果我们要学习某个物品的嵌入表示，若与该物品交互过的用户不多，那么它的梯度更新就会很慢。这就是由于数据稀疏性导致了梯度的稀疏性。

在实际应用中，对于这类出现不频繁的物品，我们肯定希望它在学习的时候，能够较大的更新步幅。而对于出现频繁的物品，我们则希望以较小的步幅进行更新。AdaGrad方法是采用历史梯度的平方和来衡量不同参数的梯度稀疏性，值越小表明越稀疏，这体现了对环境的感知能力。具体更新公式如下： $$ \begin{array}{l} h_i^t = h_i^{t-1} + (\frac{\partial L}{\partial \theta_{i}})^2 \ \ \theta_i^t = \theta_i^{t-1}-\eta \frac{1}{\sqrt{h_i^t+\epsilon}} \frac{\partial L}{\partial \theta_i} \end{array} $$

从公式中可以看出，参数 $\theta$ 的第 $i$ 个参数 $\theta_i$ 在第 $t$ 步更新时，梯度部分除了乘了一个学习率 $\eta$，还除以了自身的历史梯度的平方和 $h_i^t$ 。

• 对于更新不频繁的参数，它的历史梯度平方和 $h_i^t$ 较小，其在更新对应的梯度时，步长也就更大一些。反之，对于更新频繁的参数，它的学习步长也就更小一些。
• 但随着时间的推移，学习率都会越来越小，保证了算法最终的收敛。

3.6 RMSProp

RMSProp方法的英文全称为Root Mean Square Prop，该方法是AdaGrad的一种改进，由Geoffrey Hinton教授在教案中提出。 $$ \begin{array}{l} h_i^t = \beta h_i^{t-1} + (1-\beta)(\frac{\partial L}{\partial \theta_{i}})^2 \ \ \theta_i^t = \theta_i^{t-1}-\eta \frac{1}{\sqrt{h_i^t}+\epsilon } \frac{\partial L}{\partial \theta_i} \end{array} $$ 从公式上来看，RMSProp算法不是像AdaGrad算法那样直接的累加历史的所有平方梯度，而是加了一个衰减系数来控制历史信息的获取多少。加了一个参数 $\beta$ 之后，作用相当于加了一个衰减系数来控制历史信息的获取多少。

3.7 Adam

Adam方法Momentum和RMSProp方法的优点集于一身。

• 一方面，Adam通过记录梯度的一阶矩（first moment），即过往梯度和当前梯度的平均，来保持惯性；
• 另一方面，通过记录二阶矩（second moment）,即过往梯度的平方和当前梯度的平方的平均，这类似于AdaGrad方法，为不同的参数生成了自适应的学习率。

一阶矩和二阶矩的计算都采用类似于滑动窗口内求平均的思想，即当前梯度和近一段时间内梯度的平均值，时间久远的梯度对当前平均值的贡献呈指数型下降。

首先计算损失函数在$t$时刻的梯度值 $g_{t} = \nabla_{\theta} L_{t}\left(\theta_{t-1}\right)$，然后计算梯度的一阶矩$m_t$和二阶矩$v_t$： $$ m_t=\beta_1 m_{t-1} + (1-\beta_1) \cdot g_t \ \ v_t=\beta_2 v_{t-1} + (1-\beta_2) \cdot {g_t}^2 $$ 这里的一阶矩相当于在估计 $\mathbb{E}[g_t]$，二阶矩是在估计 $\mathbb{E}[{g_t}^2]$。从物理上来看，它们的意义为：

• 当 $||m_t||$ 大且 $v_t$ 大时，说明梯度很大并且很稳定，可能是遇到了一个较长的斜坡，此时的前进方向明确；
• 当 $||m_t||$ 趋近于 $0$ 且 $v_t$ 大时，说明此时梯度不稳定，可能遇到了一个峡谷，容易反弹震荡；
• 当 $||m_t||$ 大且 $v_t$ 趋向于 $0$ 时，这种情况不会发生；
• 当 $||m_t||$ 和 $v_t$ 趋向于 $0$ 时，说明梯度趋近于 $0$，可能到达局部最优点，也有可能陷入了平原；

在原论文中，$\beta_1$ 默认取值为 $0.9$，$\beta_2$ 默认取值为 $0.999$，而一阶矩 $m_t$ 和二阶矩 $v_t$ 初始化值为 $0$，这会导致训练初期 $m_t,v_t$ 在更新初期值会偏向于 $0$，所以要进行偏置矫正： $$ \hat{m_t} = \frac{m_t}{1 - \beta_1^t} \ \hat{v_t} = \frac{v_t}{1 - \beta_2^t} $$ 参数的更新公式为： $$ \theta_{t+1} = \theta_{t} - \frac{\eta \cdot \hat{m_t}}{\sqrt{\hat{v_t}+\epsilon }} $$

参考资料

[1] 《百面机器学习》，诸葛越著

[2] 《深度学习入门：基于Python的理论与实现》，斋藤康毅著

[3] 凸集、凸函数与凸优化基本概念：https://blog.51cto.com/u_15009309/2554110

[4] 斯坦福凸优化课件： http://cs229.stanford.edu/section/cs229-cvxopt.pdf

[5] Hessian矩阵和极值判断: https://zhuanlan.zhihu.com/p/377754969

[6] 深度学习优化入门：https://zhuanlan.zhihu.com/p/42495844

[7] 深度学习中的优化算法：https://zhuanlan.zhihu.com/p/43506482)

[8] 故意让人难记的公式——多元函数极值： https://mp.weixin.qq.com/s?__biz=MzU1OTAzMjE2OA==&mid=2247485977&idx=1&sn=c35473dcca80d0df80ed0a5951eb0a02&chksm=fc1c381ecb6bb108a0e37e40d817594eebbe8f05efe9294a8a164d632d3a1e1eab3a33c4ede2&token=2002571029&lang=zh_CN#rd)