 PNN
PNN
# PNN
# 1. 动机
在特征交叉的相关模型中FM, FFM都证明了特征交叉的重要性,FNN将神经网络的高阶隐式交叉加到了FM的二阶特征交叉上,一定程度上说明了DNN做特征交叉的有效性。但是对于DNN这种“add”操作的特征交叉并不能充分挖掘类别特征的交叉效果。PNN虽然也用了DNN来对特征进行交叉组合,但是并不是直接将低阶特征放入DNN中,而是设计了Product层先对低阶特征进行充分的交叉组合之后再送入到DNN中去。
PNN模型其实是对IPNN和OPNN的总称,两者分别对应的是不同的Product实现方法,前者采用的是inner product,后者采用的是outer product。在PNN的算法方面,比较重要的部分就是Product Layer的简化实现方法,需要在数学和代码上都能够比较深入的理解。
# 2. 模型的结构及原理
在学习PNN模型之前,应当对于DNN结构具有一定的了解,同时已经学习过了前面的章节。
PNN模型的整体架构如下图所示:
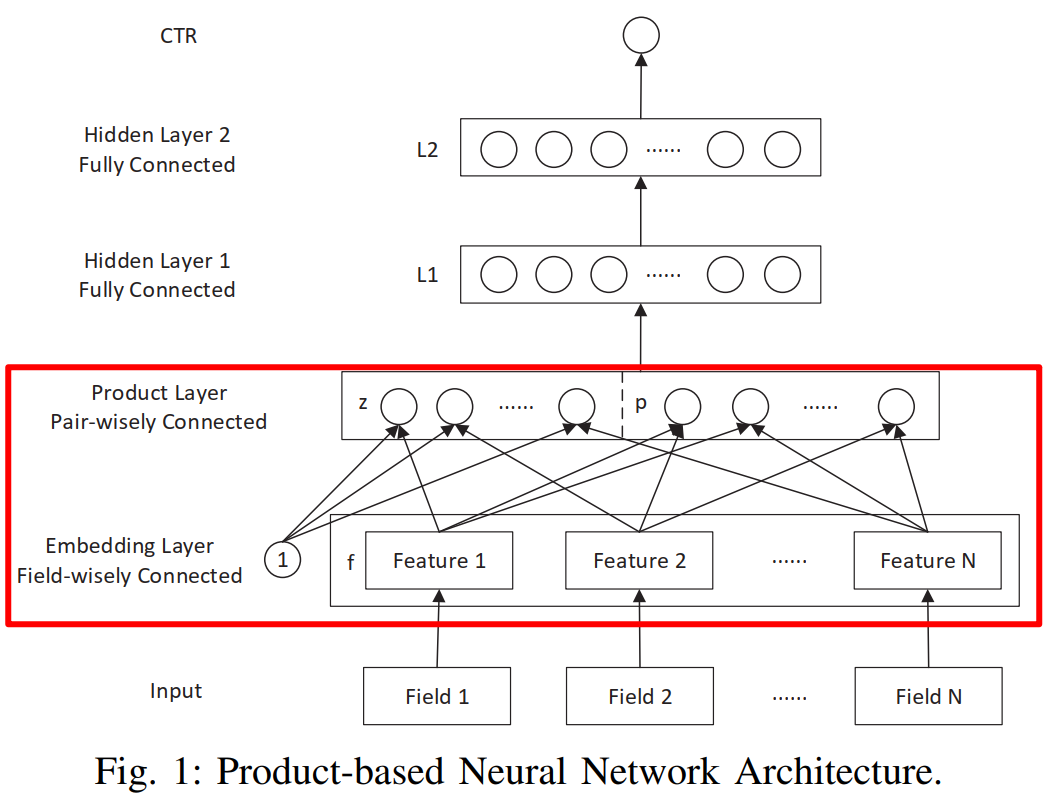
一共分为五层,其中除了Product Layer别的layer都是比较常规的处理方法,均可以从前面的章节进一步了解。模型中最重要的部分就是通过Product层对embedding特征进行交叉组合,也就是上图中红框所显示的部分。
Product层主要有线性部分和非线性部分组成,分别用$l_z$和$l_p$来表示,
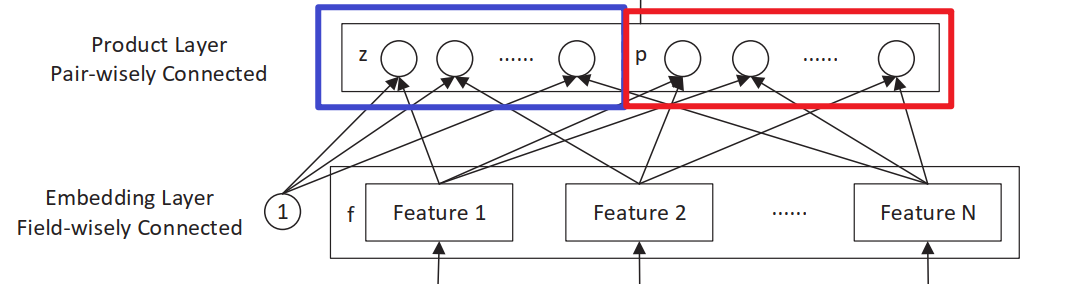
- 线性模块,一阶特征(未经过显示特征交叉处理),对应论文中的$l_z=(l_z^1,l_z^2, ..., l_z^{D_1})$
- 非线性模块,高阶特征(经过显示特征交叉处理),对应论文中的$l_p=(l_p^1,l_p^2, ..., l_p^{D_1})$
==线性部分==
先来解释一下$l_z$是如何计算得到的,在介绍计算$l_z$之前先介绍一下矩阵内积计算, 如下公式所示,用一句话来描述就是两个矩阵对应元素相称,然后将相乘之后的所有元素相加 $$ A \odot{B} = \sum_{i,j}A_{i,j}B_{i,j} $$ $l_z^n$的计算就是矩阵内积,而$l_z$是有$D_1$个$l_z^n$组成,所以需要$D1$个矩阵求得,但是在代码实现的时候不一定是定义$D_1$个矩阵,可以将这些矩阵Flatten,具体的细节可以参考给出的代码。 $$ l_z=(l_z^1,l_z^2, ..., l_z^{D_1})\ l_z^n = W_z^n \odot{z} \ z = (z_1, z_2, ..., z_N) $$ 总之这一波操作就是将所有的embedding向量中的所有元素都乘以一个矩阵的对应元素,最后相加即可,这一部分比较简单(N表示的是特征的数量,M表示的是所有特征转化为embedding之后维度,也就是N*emb_dim) $$ l_z^n = W_z^n \odot{z} = \sum_{i=1}^N \sum_{j=1}^M (W_z^n){i,j}z{i,j} $$
# 2.1 Product Layer
==非线性部分==
上面介绍了线性部分$l_p$的计算,非线性部分的计算相比线性部分要复杂很多,先从整体上看$l_p$的计算 $$ l_p=(l_p^1,l_p^2, ..., l_p^{D_1}) \ l_p^n = W_p^n \odot{p} \ p = {p_{i,j}}, i=1,2,...,N,j=1,2,...,N $$ 从上述公式中可以发现,$l_p^n$和$l_z^n$类似需要$D_1$个$W_p^n$矩阵计算内积得到,重点就是如何求这个$p$,这里作者提出了两种方式,一种是使用内积计算,另一种是使用外积计算。
# 2.1.1 IPNN
使用内积实现特征交叉就和FM是类似的(两两向量计算内积),下面将向量内积操作表示如下表达式 $$ g(f_i,f_j) = <f_i, f_j> $$ 将内积的表达式带入$l_p^n$的计算表达式中有: $$ \begin{align}
l_p^n &= W_p^n \odot{p} \ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n){i,j}p{i,j} \ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}<f_i, f_j>
\end{align} $$ 上面就提到了这里使用的内积是计算两两特征之间的内积,然而向量a和向量b的内积与向量b和向量a的内积是相同的,其实是没必要计算的,看一下下面FM的计算公式: $$ \hat{y}(X) = \omega_{0}+\sum_{i=1}^{n}{\omega_{i}x_{i}}+\sum_{i=1}^{n}{\sum_{j=i+1}^{n} <v_{i},v_{j}>x_{i}x_{j}} $$ 也就是说计算的内积矩阵$p$是对称的,那么与其对应元素做矩阵内积的矩阵$W_p^n$也是对称的,对于可学习的权重来说如果是对称的是不是可以只使用其中的一半就行了呢,所以基于这个思考,对Inner Product的权重定义及内积计算进行优化,首先将权重矩阵分解$W_p^n=\theta^n \theta^{nT}$,此时$\theta^n \in R^N$(参数从原来的$N^2$变成了$N$),将分解后的$W_p^n$带入$l_p^n$的计算公式有: $$ \begin{align}
l_p^n &= W_p^n \odot{p} \ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n){i,j}p{i,j} \ &= \sum_{i=1}^N \sum_{j=1}^N \theta^n \theta^n <f_i, f_j> \ &= \sum_{i=1}^N \sum_{j=1}^N <\theta^n f_i, \theta^n f_j> \ &= <\sum_{i=1}^N \theta^n f_i, \sum_{j=1}^N \theta^n f_j> \ &= ||\sum_{i=1}^N \theta^n f_i||^2 \end{align} $$ 所以优化后的$l_p$的计算公式为: $$ l_p = (||\sum_{i=1}^N \theta^1 f_i||^2, ||\sum_{i=1}^N \theta^2 f_i||^2, ..., ||\sum_{i=1}^N \theta^{D_1} f_i||^2) $$ 这里为了好理解不做过多的解释,其实这里对于矩阵分解省略了一些细节,感兴趣的可以去看原文,最后模型实现的时候就是基于上面的这个公式计算的(给出的代码也是基于优化之后的实现)。
# 2.1.2 OPNN
使用外积实现相比于使用内积实现,唯一的区别就是使用向量的外积来计算矩阵$p$,首先定义向量的外积计算 $$ g(i,j) = f_i f_j^T $$ 从外积公式可以发现两个向量的外积得到的是一个矩阵,与上面介绍的内积计算不太相同,内积得到的是一个数值。内积实现的Product层是将计算得到的内积矩阵,乘以一个与其大小一样的权重矩阵,然后求和,按照这个思路的话,通过外积得到的$p$计算$W_p^n \odot{p}$相当于之前的内积值乘以权重矩阵对应位置的值求和就变成了,外积矩阵乘以权重矩阵中对应位置的子矩阵然后将整个相乘得到的大矩阵对应元素相加,用公式表示如下: $$ \begin{align}
l_p^n &= W_p^n \odot{p} \ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n){i,j}p{i,j} \ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j} f_i f_j^T
\end{align} $$ 需要注意的是此时的$(W_p^n){i,j}$表示的是一个矩阵,而不是一个值,此时计算$l_p$的复杂度是$O(D_1N^2M^2)$, 其中$N^2$表示的是特征的组合数量,$M^2$表示的是计算外积的复杂度。这样的复杂度肯定是无法接受的,所以为了优化复杂度,PNN的作者重新定义了$p$的计算方式: $$ p=\sum{i=1}^N \sum_{j=1}^N f_i f_j^T = f_{\sum}(f_\sum)^T\ f_\sum = \sum_{i=1}^N f_i $$ 需要注意,这里新定义的外积计算与传统的外积计算时不等价的,这里是为了优化计算效率重新定义的计算方式,从公式中可以看出,相当于先将原来的embedding向量在特征维度上先求和,变成一个向量之后再计算外积。加入原embedding向量表示为$E \in R^{N\times M}$,其中$N$表示特征的数量,M表示的是所有特征的总维度,即$Nemb_dim$, 在特征维度上进行求和就是将$E \in R^{N\times M}$矩阵压缩成了$E \in R^M$, 然后两个$M$维的向量计算外积得到最终所有特征的外积交叉结果$p\in R^{M\times M}$,最终的$l_p^n$可以表示为: $$ l_p^n = W_p^n \odot{p} = \sum_{i=1}^N \sum_{j=1}^N (W_p^n){i,j}p{i,j} \ $$ 最终的计算方式和$l_z$的计算方式看起来差不多,但是需要注意外积优化后的$W_p^n$的维度是$R^{M \times M}$的,$M$表示的是特征矩阵的维度,即$Nemb_dim$。
虽然叠加概念的引入可以降低计算开销,但是中间的精度损失也是很大的,性能与精度之间的tradeoff
# 3. 代码实现
代码实现的整体逻辑比较简单,就是对类别特征进行embedding编码,然后通过embedding特征计算$l_z,l_p$, 接着将$l_z, l_p$的输出concat到一起输入到DNN中得到最终的预测结果
def PNN(dnn_feature_columns, inner=True, outer=True):
# 构建输入层,即所有特征对应的Input()层,这里使用字典的形式返回,方便后续构建模型
_, sparse_input_dict = build_input_layers(dnn_feature_columns)
# 构建模型的输入层,模型的输入层不能是字典的形式,应该将字典的形式转换成列表的形式
# 注意:这里实际的输入与Input()层的对应,是通过模型输入时候的字典数据的key与对应name的Input层
input_layers = list(sparse_input_dict.values())
# 构建维度为k的embedding层,这里使用字典的形式返回,方便后面搭建模型
embedding_layer_dict = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)
sparse_embed_list = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=False)
dnn_inputs = ProductLayer(units=32, use_inner=True, use_outer=True)(sparse_embed_list)
# 输入到dnn中,需要提前定义需要几个残差块
output_layer = get_dnn_logits(dnn_inputs)
model = Model(input_layers, output_layer)
return model
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
PNN的难点就是Product层的实现,下面是Product 层实现的代码,代码中是使用优化之后$l_p$的计算方式编写的, 代码中有详细的注释,但是要完全理解代码还需要去理解上述说过的优化思路。
class ProductLayer(Layer):
def __init__(self, units, use_inner=True, use_outer=False):
super(ProductLayer, self).__init__()
self.use_inner = use_inner
self.use_outer = use_outer
self.units = units # 指的是原文中D1的大小
def build(self, input_shape):
# 需要注意input_shape也是一个列表,并且里面的每一个元素都是TensorShape类型,
# 需要将其转换成list然后才能参与数值计算,不然类型容易错
# input_shape[0] : feat_nums x embed_dims
self.feat_nums = len(input_shape)
self.embed_dims = input_shape[0].as_list()[-1]
flatten_dims = self.feat_nums * self.embed_dims
# Linear signals weight, 这部分是用于产生Z的权重,因为这里需要计算的是两个元素对应元素乘积然后再相加
# 等价于先把矩阵拉成一维,然后相乘再相加
self.linear_w = self.add_weight(name='linear_w', shape=(flatten_dims, self.units), initializer='glorot_normal')
# inner product weight
if self.use_inner:
# 优化之后的内积权重是未优化时的一个分解矩阵,未优化时的矩阵大小为:D x N x N
# 优化后的内积权重大小为:D x N
self.inner_w = self.add_weight(name='inner_w', shape=(self.units, self.feat_nums), initializer='glorot_normal')
if self.use_outer:
# 优化之后的外积权重大小为:D x embed_dim x embed_dim, 因为计算外积的时候在特征维度通过求和的方式进行了压缩
self.outer_w = self.add_weight(name='outer_w', shape=(self.units, self.embed_dims, self.embed_dims), initializer='glorot_normal')
def call(self, inputs):
# inputs是一个列表
# 先将所有的embedding拼接起来计算线性信号部分的输出
concat_embed = Concatenate(axis=1)(inputs) # B x feat_nums x embed_dims
# 将两个矩阵都拉成二维的,然后通过矩阵相乘得到最终的结果
concat_embed_ = tf.reshape(concat_embed, shape=[-1, self.feat_nums * self.embed_dims])
lz = tf.matmul(concat_embed_, self.linear_w) # B x units
# inner
lp_list = []
if self.use_inner:
for i in range(self.units):
# 相当于给每一个特征向量都乘以一个权重
# self.inner_w[i] : (embed_dims, ) 添加一个维度变成 (embed_dims, 1)
delta = tf.multiply(concat_embed, tf.expand_dims(self.inner_w[i], axis=1)) # B x feat_nums x embed_dims
# 在特征之间的维度上求和
delta = tf.reduce_sum(delta, axis=1) # B x embed_dims
# 最终在特征embedding维度上求二范数得到p
lp_list.append(tf.reduce_sum(tf.square(delta), axis=1, keepdims=True)) # B x 1
# outer
if self.use_outer:
# 外积的优化是将embedding矩阵,在特征间的维度上通过求和进行压缩
feat_sum = tf.reduce_sum(concat_embed, axis=1) # B x embed_dims
# 为了方便计算外积,将维度进行扩展
f1 = tf.expand_dims(feat_sum, axis=2) # B x embed_dims x 1
f2 = tf.expand_dims(feat_sum, axis=1) # B x 1 x embed_dims
# 求外积, a * a^T
product = tf.matmul(f1, f2) # B x embed_dims x embed_dims
# 将product与外积权重矩阵对应元素相乘再相加
for i in range(self.units):
lpi = tf.multiply(product, self.outer_w[i]) # B x embed_dims x embed_dims
# 将后面两个维度进行求和,需要注意的是,每使用一次reduce_sum就会减少一个维度
lpi = tf.reduce_sum(lpi, axis=[1, 2]) # B
# 添加一个维度便于特征拼接
lpi = tf.expand_dims(lpi, axis=1) # B x 1
lp_list.append(lpi)
# 将所有交叉特征拼接到一起
lp = Concatenate(axis=1)(lp_list)
# 将lz和lp拼接到一起
product_out = Concatenate(axis=1)([lz, lp])
return product_out
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
因为这个模型的整体实现框架比较简单,就不画实现的草图了,直接看模型搭建的函数即可,对于PNN重点需要理解Product的两种类型及不同的优化方式。
下面是一个通过keras画的模型结构图,为了更好的显示,类别特征都只是选择了一小部分,画图的代码也在github中。
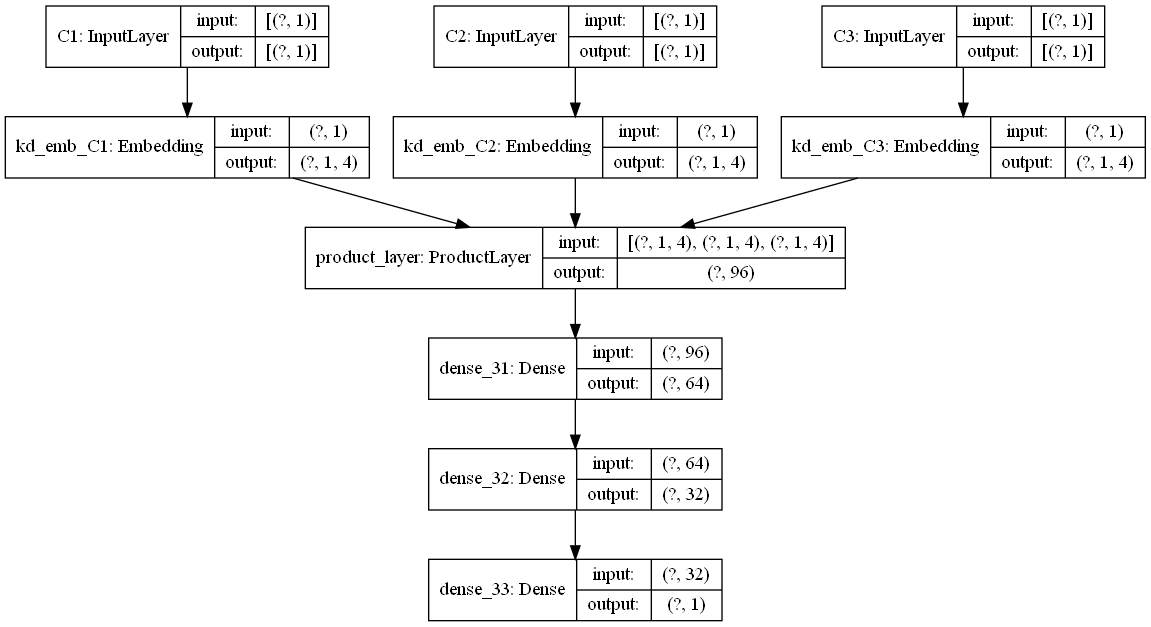
# 4. 思考题
- 降低复杂度的具体策略与具体的product函数选择有关,IPNN其实通过矩阵分解,“跳过”了显式的product层,而OPNN则是直接在product层入手进行优化。看原文去理解优化的动机及细节。
