 NeuralCF
NeuralCF
# NeuralCF
# 1.动机
在前面的组队学习中,我们学习了最经典的推荐算法,协同过滤。在前深度学习的时代,协同过滤曾经大放异彩,但随着技术的发展,协同过滤相比深度学习模型的弊端就日益显现出来了,因为它是通过直接利用非常稀疏的共现矩阵进行预测的,所以模型的泛化能力非常弱,遇到历史行为非常少的用户,就没法产生准确的推荐结果了。虽然,我们可以通过矩阵分解算法增强它的泛化能力,但因为矩阵分解是利用非常简单的内积方式来处理用户向量和物品向量的交叉问题的,所以,它的拟合能力也比较弱。这该怎么办呢?不是说深度学习模型的拟合能力都很强吗?我们能不能利用深度学习来改进协同过滤算法呢?当然是可以的。2017 年,新加坡国立的研究者就使用深度学习网络来改进了传统的协同过滤算法,取名 NeuralCF(神经网络协同过滤)。NeuralCF 大大提高了协同过滤算法的泛化能力和拟合能力,让这个经典的推荐算法又重新在深度学习时代焕发生机。这章节,我们就一起来学习并实现 NeuralCF!
# 2.模型结构及原理
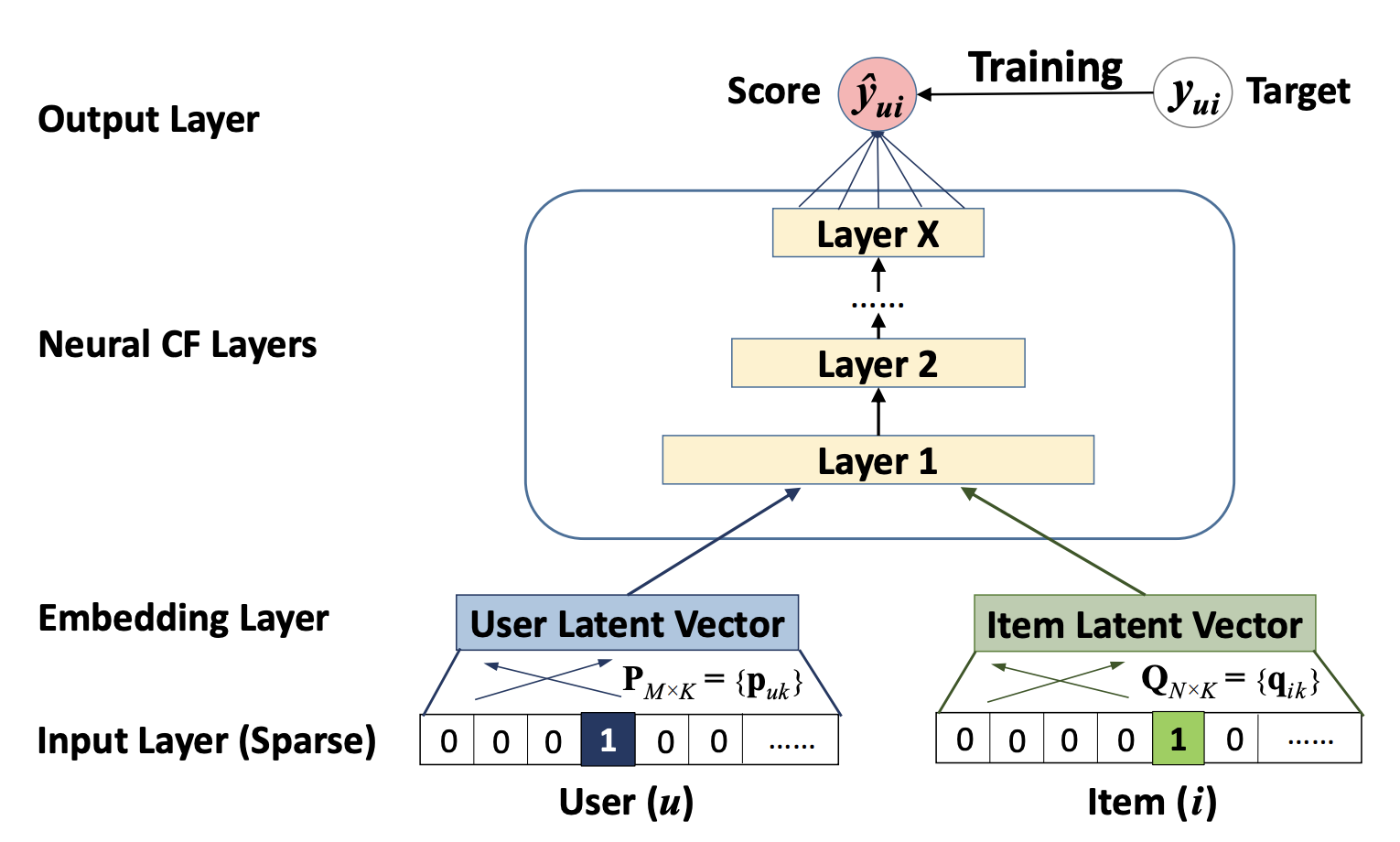
Neural collaborative filtering framework
为了允许神经网络对协同过滤进行一个完整的处理,我们采用上图展示的多层感知机去模拟一个用户项目交互$y_{ui}$,它的一层的输出作为下一层的输入。底部输入层包括两个特征向量$v^U_u$和$v^I_i$ ,分别用来描述用户$u$和项目$i$。 他们可以进行定制,用以支持广泛的用户和项目的建模,例如上下文感知,基于内容,和基于邻居的构建方式。由于本章工作的重点是纯的协同过滤模型设置,我们仅使用一个用户和一个项目作为输入特征,它使用$one-hot$编码将它们转化为二值化稀疏向量。注意到,我们对输入使用这样的通用特征表示,可以很容易地使用的内容特征来表示用户和项目,以调整解决冷启动问题。
输入层上面是嵌入层$(Embedding Layer)$;它是一个全连接层,用来将输入层的稀疏特征向量映射为一个稠密向量$(dense vector)$。所获得的用户(项目)的嵌入(就是一个稠密向量)可以被看作是在潜在因素模型的上下文中用于描述用户(项目)的潜在向量。然后我们将用户嵌入和项目嵌入送入多层神经网络中,我们将它称为神经网络协同过滤层,它将潜在向量映射为预测分数。NCF层的每一层都可以被定制,用以发现用户-项目交互的某些潜在结构。最后一个隐藏层 $X$ 的维度尺寸决定了模型的能力。最终输出层是预测分数$\hat{y}{ui}$,通过最小化预测值$\hat{y}{ui}$和其目标值$y_{ui}$之间逐点损失进行训练。
论文中主要运用均方误差$(squared loss)$进行回归: $$ L_{sqr}=\sum_{(u,i)\in y\cup y^-}w_{ui}(y_{ui}-\hat{y}{ui})^2 $$ 其中$ y$表示交互矩阵$Y$中观察到的条目(如对电影有明确的评分,评级), $y^-$表示负样本($negative instances$,可以将未观察的样本全体视为负样本,或者采取抽样的方式标记为负样本); $w{ui}$是一个超参数,用来表示训练样本$(u,i)$的权重。虽然均方误差可以通过假设观测服从高斯分布来作出解释,但是它不适合处理隐性数据$(implicit data)$。这是因为对于隐含数据来说,目标值 $y_{ui}$是二进制值$1$或$0$,表示$u$是否与$i$进行了互动。在下文中提出了逐点学习NCF的概率学方法,特别注重隐性数据的二进制属性。
考虑到隐性反馈的一类性质,我们可以将$y_{ui}$的值作为一个标签------$1$表示项目$i$和用户$u$相关,$0$表达不相关。这样一来预测分数$\hat{y}{ui}$就代表了项目$i$和用户$u$相关的可能性大小。为了赋予NCF这样的概率解释,我们需要将网络输出限制到$[0,1]$的范围内,通过使用概率函数(逻辑函数$sigmoid$或者$probit$函数)作为激活函数作用在输出层$\phi{out}$,我们可以很容易地实现数据压缩。经过以上设置后,我们这样定义似然函数: $$ p(y,y^-|P,Q,\Theta_f)=\prod_{(u,i)\in{y}}\hat{y}{ui}\prod{(u,j)\in{y^-}}(1-\hat{y}{uj}) $$ 对似然函数取负对数,我们得到(负对数可以用来表示$Loss$函数,而且还能消除小数乘法的下溢出问题): $$ L=-\sum{(u,i)\in{y}}log\hat{y}{ui}-\sum{(u,j)\in{y^-}}log(1-\hat{y}{uj})=-\sum{(u,i)\in{y}\cup{y}^-}y_{ui}log \hat{y}{ui}+(1-y{ui})log(1-\hat{y}_{ui}) $$ 这是NCF需要去最小化的目标函数,并且可以通过使用随机梯度下降$(SGD)$来进行训练优化。这个函数和交叉熵损失函数$(binary cross-entropy loss,又被成为log loss)$是一样的。通过在NCF上使用这样一个概率处理$(probabilistic treatment)$,我们把隐性反馈的推荐问题当做一个二分类问题来解决。对于负样本 $y^-$ ,我们在每次迭代均匀地从未观察到的相互作用中采样(作为负样本)并且对照可观察到交互的数量,控制采样比率。
我们现在来证明MF是如何被解释为我们的NCF框架的一个特例。由于MF是推荐领域最流行的模型,并已在众多文献中被广泛的研究,复现它能证明NCF可以模拟大部分的分解模型。由于输入层是用户(项目)ID中的一个$one-hot encoding$编码,所获得的嵌入向量可以被看作是用户(项目)的潜在向量。我们用$P^Tv^U_u$表示用户的潜在向量$p_u$,$Q^Tv^I_i$表示项目的潜在向量$q_i$ ,我们定义第一层神经CF层的映射函数为: $$ \phi(p_u,q_i)=p_u\odot q_i $$ 其中$\odot$表示向量的逐元素乘积。然后,我们将向量映射到输出层: $$ \hat{y}{ui}=a{out}(h^T(p_u\odot q_i)) $$ 其中$a_{out}$和$h$分别表示输出层的激活函数和连接权。直观地讲,如果我们将$a_{out}$看做一个恒等函数, $h$权重全为1,显然这就是我们的MF模型。在NCF的框架下,MF可以很容易地被泛化和推广。例如,如果我们允许从没有一致性约束(uniform constraint)的数据中学习$h$,则会形成MF的变体,它允许潜在维度的不同重要性(For example, if we allow h to be learnt from data without the uniform constraint, it will result in a variant of MF that allows varying importance of latent dimensions)。如果我们用一个非线性函数$a_{out}$将进一步推广MF到非线性集合,使得模型比线性MF模型更具有表现力。在NCF下实现一个更一般化的MF,它使用Sigmoid函数$\sigma(x)=1/1(1+e^{-x})$作为激活函数,通过$log loss$学习 $h$。称为GMF(Generalized Matrix Factorization,广义矩阵分解)。

GMF,它应用了一个线性内核来模拟潜在的特征交互;MLP,使用非线性内核从数据中学习交互函数。接下来的问题是:我们如何能够在NCF框架下融合GMF和MLP,使他们能够相互强化,以更好地对复杂的用户-项目交互建模?一个直接的解决方法是让GMF和MLP共享相同的嵌入层(Embedding Layer),然后再结合它们分别对相互作用的函数输出。这种方式和著名的神经网络张量(NTN,Neural Tensor Network)有点相似。然而,共享GMF和MLP的嵌入层可能会限制融合模型的性能。例如,它意味着,GMF和MLP必须使用的大小相同的嵌入;对于数据集,两个模型的最佳嵌入尺寸差异很大,使得这种解决方案可能无法获得最佳的组合。为了使得融合模型具有更大的灵活性,我们允许GMF和MLP学习独立的嵌入,并结合两种模型通过连接他们最后的隐层输出。
# 3.代码实现
从模型的结构上来看,NeuralCF的模型其实是在矩阵分解上进行了加强,用MLP代替了inner product,下面是构建模型的核心代码,详细代码参考github。
def NCF(dnn_feature_columns):
# 构建输入层,即所有特征对应的Input()层,这里使用字典的形式返回,方便后续构建模型
_, sparse_input_dict = build_input_layers(dnn_feature_columns) # 没有dense特征
# 构建模型的输入层,模型的输入层不能是字典的形式,应该将字典的形式转换成列表的形式
# 注意:这里实际的输入与Input()层的对应,是通过模型输入时候的字典数据的key与对应name的Input层
input_layers = list(sparse_input_dict.values())
# 创建两份embedding向量, 由于Embedding层的name不能相同,所以这里加入一个prefix参数
GML_embedding_dict = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False, prefix='GML')
MLP_embedding_dict = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False, prefix='MLP')
# 构建GML的输出
GML_user_emb = Flatten()(GML_embedding_dict['user_id'](sparse_input_dict['user_id'])) # B x embed_dim
GML_item_emb = Flatten()(GML_embedding_dict['movie_id'](sparse_input_dict['movie_id'])) # B x embed_dim
GML_out = tf.multiply(GML_user_emb, GML_item_emb) # 按元素相乘
# 构建MLP的输出
MLP_user_emb = Flatten()(MLP_embedding_dict['user_id'](sparse_input_dict['user_id'])) # B x embed_dim
MLP_item_emb = Flatten()(MLP_embedding_dict['movie_id'](sparse_input_dict['movie_id'])) # B x embed_dim
MLP_dnn_input = Concatenate(axis=1)([MLP_user_emb, MLP_item_emb]) # 两个向量concat
MLP_dnn_out = get_dnn_out(MLP_dnn_input, (32, 16))
# 将dense特征和Sparse特征拼接到一起
concat_out = Concatenate(axis=1)([GML_out, MLP_dnn_out])
# 输入到dnn中,需要提前定义需要几个残差块
# output_layer = Dense(1, 'sigmoid')(concat_out)
output_layer = Dense(1)(concat_out)
model = Model(input_layers, output_layer)
return model
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
为了方便大家的阅读,我们这里还给大家画了一个整体的模型架构图,帮助大家更好的了解每一块以及前向传播。
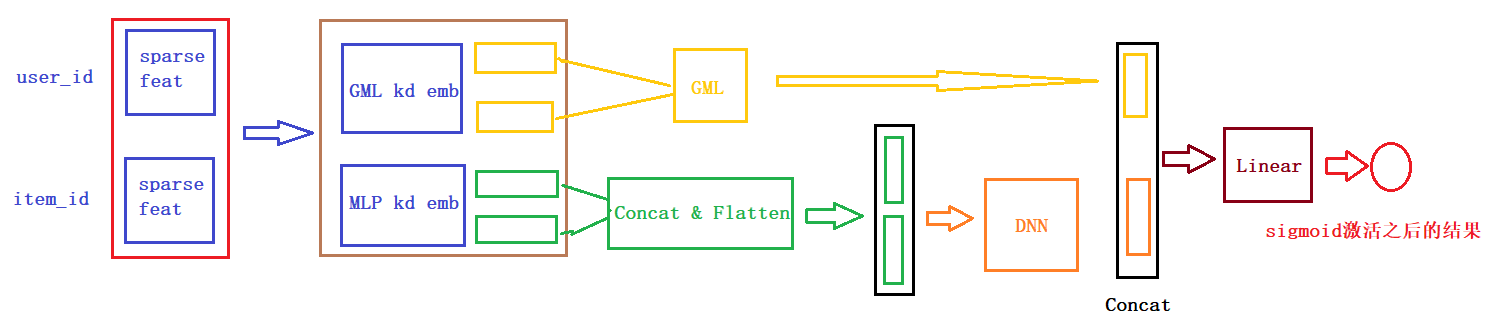
下面是一个通过keras画的模型结构图,为了更好的显示,数值特征和类别特征都只是选择了一小部分,画图的代码也在github中。

# 4.思考
如何用双塔结构实现NeuralCF?
# 5.参考资料
AI上推荐 之 NeuralCF与PNN模型(改变特征交叉方式) (opens new window)
论文笔记:Neural Collaborative Filtering(NCF) (opens new window)
datawhale组队学习之协同过滤 (opens new window)
